ที่มา: http://www.school.net.th/library/snet3/jee/slope/Slope.htm

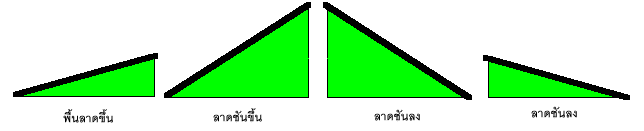
การวัดความลาดชันหรือความชัน (slope) สามารถวัดความลาดชันได้ดังรูปกราฟ

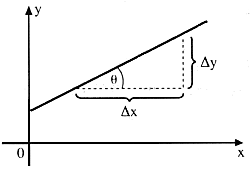
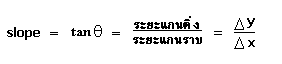
ที่มา: http://www.school.net.th/library/snet3/jee/slope/Slope.htm

ถ้าเป็นเส้นตรงขนานกับแกนนอน จะได้ว่า slope มีค่าเท่ากับศูนย์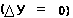 

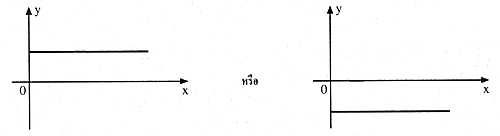
ที่มา: http://www.school.net.th/library/snet3/jee/slope/Slope.htm

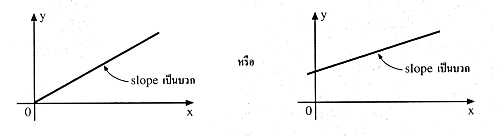
ถ้าเป็นเส้นตรงเอียงซ้ายหรือเอียงขวา จะได้ว่า slope มีค่าคงที่

- ถ้ากราฟเอียงขวา จะได้ว่า slope คงที่บวก (+) ดังรูป

- ถ้ากราฟเอียงซ้าย จะได้ว่า slope คงที่ลบ (-)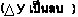

ที่มา: http://www.school.net.th/library/snet3/jee/slope/Slope.htm

                      สำหรับเส้นโค้ง การหาความชันของเส้นโค้งที่จุดใด ๆให้ลากเส้นสัมผัสกับเส้นโค้งที่จุดนั้นแล้วหาความชันของเส้นสัมผัส จะเป็นความชันของเส้นโค้งที่จุดนั้น

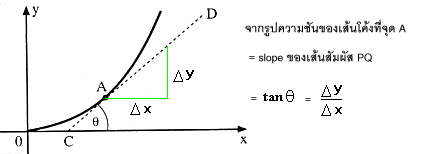
ที่มา: http://www.school.net.th/library/snet3/jee/slope/Slope.htm

จากรูป

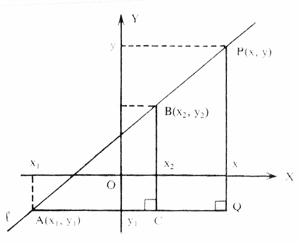
ตัวอย่างที่ 1

สูตรการสมการเส้นตรง 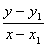      =   m  เมื่อกำหนด (x,y)  เป็นจุดบนเส้นตรง A
จะได้   y1  = 5 ,  x1  =  3    m , =   6  แทนค่า 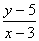     =   6
                                    y  -   5    =  6(x-3)
                                    y  - 5  =  6x – 18
ตอบ  สมการเส้นตรงที่ผ่านจุด A (3,5) มีความชันเท่ากับ 6 คือ 6x –y – 13  =  0

ตัวอย่างที่ 2

สูตรการสมการเส้นตรง 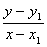      =   m  เมื่อกำหนด (x,y)  เป็นจุดบนเส้นตรง B
จะได้   y1  = -4 ,  x1  =  2    m , =   6  แทนค่า      =   -;    =  -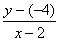
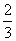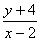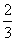
            3(y+4)   =  -2(x – 2)
            3y + 12    =  -2x + 4
           2x + 3y +  8  =  0
จงหาระยะห่างระหว่างจุด (6,-5) ไปยังเส้นตรง  6x -8y - 5  =  0
ตอบ  สมการเส้นตรงที่ผ่านจุด B (2,-4) มีความชันเท่ากับ - 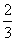 คือ 2x + 3y +  8  =  0

ตัวอย่างที่ 3

กำหนดให้ความชันของเส้นตรงที่ต้องการเป็น  x  จะได้   x. –3   -1;    x  =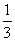  
สูตรการสมการเส้นตรง 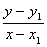      =   m  เมื่อกำหนด (x,y)  เป็นจุดบนเส้นตรง C
จะได้   y1  = -4 ,  x1  =  -6    m , = 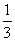    แทนค่า      =   ; =
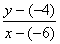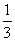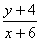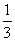
            3(y+4)            =   x+6
           3y + 12           =   x + 6
             x – 3y -  6        =   0
ตอบ  สมการเส้นตรงที่ผ่านจุด C (-6,-4) ตั้งฉากกับเส้นตรงที่มีความชัน –3 คือ  x – 3y – 6  =  0