 การแปรผัน (variation) คือ ความสัมพันธ์ระหว่างปริมาณสองปริมาณหรือมากกว่านั้น เมื่อปริมาณหนึ่งเปลี่ยนแปลงไป อีกปริมาณหนึ่งจะเปลี่ยนตามไปด้วย อย่างได้สัดส่วนกัน สามารถแบ่งการแปรผันออกเป็น 3 ชนิด คือ การแปรผัน (variation) คือ ความสัมพันธ์ระหว่างปริมาณสองปริมาณหรือมากกว่านั้น เมื่อปริมาณหนึ่งเปลี่ยนแปลงไป อีกปริมาณหนึ่งจะเปลี่ยนตามไปด้วย อย่างได้สัดส่วนกัน สามารถแบ่งการแปรผันออกเป็น 3 ชนิด คือ
1. การแปรผันตรง (direct variation)
2. การแปรผกผัน (inverse variation)
3. การแปรผันเกี่ยวเนื่อง (joint variation)
 การแก้ปัญหาโจทย์การแปรผัน การแก้ปัญหาโจทย์การแปรผัน
1. พิจารณาว่ามีสิ่งที่เกี่ยวข้องกันอยู่กี่สิ่ง กำหนดตัวแปร เท่ากับจำนวนสิ่งที่เกี่ยวข้องกันตามโจทย์ และเขียนหน่วย
2. สร้างสมการแปรผัน แล้วเปลี่ยนเป็นสมการที่มีค่าคงตัว (นิยมใช้ค่า k)
3. แทนค่าตัวแปร เพื่อแก้สมการหาค่า k
4. เขียนสมการโดยแทนค่า k แล้วหาค่าที่โจทย์ถาม
การแปรผันตรง
 การแปรผันตรง (direct variation) เป็นความสัมพันธ์ระหว่างของสองสิ่งหรือปริมาณสองปริมาณ เมื่อสิ่งหนึ่งเพิ่มอีกสิ่งหนึ่งก็เพิ่มขึ้นตามไปด้วยอย่างเป็นสัดส่วนกัน หรือเมื่อสิ่งหนึ่งลดอีกสิ่งหนึ่งก็ลดลงตามไปด้วยอย่างเป็นสัดส่วนกัน เรียกว่า การแปรผันตามกัน หรือ การแปรผันตรง หรือ เป็นสัดส่วนโดยตรง การแปรผันตรง (direct variation) เป็นความสัมพันธ์ระหว่างของสองสิ่งหรือปริมาณสองปริมาณ เมื่อสิ่งหนึ่งเพิ่มอีกสิ่งหนึ่งก็เพิ่มขึ้นตามไปด้วยอย่างเป็นสัดส่วนกัน หรือเมื่อสิ่งหนึ่งลดอีกสิ่งหนึ่งก็ลดลงตามไปด้วยอย่างเป็นสัดส่วนกัน เรียกว่า การแปรผันตามกัน หรือ การแปรผันตรง หรือ เป็นสัดส่วนโดยตรง
 บทนิยาม กำหนดให้ บทนิยาม กำหนดให้  และ และ 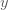 แทนปริมาณใด ๆ แทนปริมาณใด ๆ 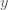 แปรผันตรงกับ แปรผันตรงกับ  ใช้สัญลักษณ์ ใช้สัญลักษณ์ 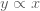 เขียนในรูปสมการเป็น เขียนในรูปสมการเป็น 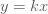 เมื่อ เมื่อ 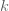 เป็นค่าคงตัว และ เป็นค่าคงตัว และ 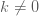 เรียก เรียก 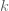 ว่า ค่าคงตัวแห่งการแปรผัน (variation constant) ว่า ค่าคงตัวแห่งการแปรผัน (variation constant)
ตัวอย่างที่ 1 ถ้า 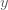 แปรผันโดยตรงกับ แปรผันโดยตรงกับ  กำหนด กำหนด 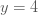 เมื่อ เมื่อ 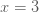 จงหาค่า จงหาค่า 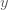 เมื่อ เมื่อ 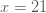
วิธีทำ
จาก 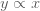 จะได้ จะได้ 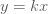 (เมื่อ (เมื่อ 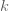 เป็นค่าคงตัว) เป็นค่าคงตัว)
แทนค่า 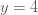 เมื่อ เมื่อ 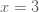 ใน ใน 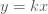 จะได้ จะได้
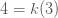 → → 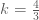
จะได้ 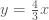
แทนค่า 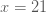 จะได้ จะได้ 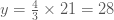 ตอบ ตอบ
ตัวอย่างที่ 2 ถ้า  แปรผันตามกำลังสองของ แปรผันตามกำลังสองของ 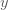 และ และ 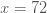 เมื่อ เมื่อ 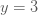 จงหาค่าคงตัวของการแปรผัน และค่าของ จงหาค่าคงตัวของการแปรผัน และค่าของ 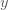 เมื่อ เมื่อ 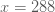
วิธีทำ  แปรผันตามกำลังสองของ แปรผันตามกำลังสองของ 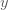 คือ คือ 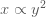
จะได้ 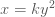 (เมื่อ (เมื่อ 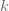 เป็นค่าคงตัว) เป็นค่าคงตัว)
แทนค่า 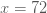 เมื่อ เมื่อ 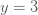 ใน ใน 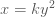
จะได้ 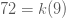 → → 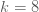
ดังนั้น จะได้สมการเป็น 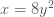
ถ้า 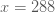 ค่า ค่า 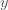 คือ คือ 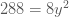
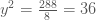
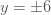 ตอบ ตอบ
ตัวอย่างที่ 3 ความยาวของก้านลูกตุ้มนาฬิกา แปรผันตามกำลังสองของเวลาแกว่งครบรอบ ถ้าก้านลูกตุ้มนาฬิกายาว 99.2 เซนติเมตร จะแกว่งครบรอบใน 2 วินาที ก้านของลูกตุ้มต้องยาวกี่เซนติเมตร จึงจะแกว่งได้นาทีละ 24 รอบ
วิธีทำ
กำหนดให้ 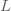 เป็นความยาวของก้านลูกตุ้มนาฬิกา หน่วยเป็น เซนติเมตร เป็นความยาวของก้านลูกตุ้มนาฬิกา หน่วยเป็น เซนติเมตร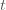 เป็นเวลาแกว่งครบรอบของลูกตุ้ม หน่วยเป็น วินาที เป็นเวลาแกว่งครบรอบของลูกตุ้ม หน่วยเป็น วินาที
จากโจทย์ 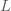 แปรผันตามกำลังสองของ แปรผันตามกำลังสองของ 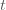 คือ คือ 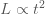
จะได้ 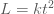 (เมื่อ (เมื่อ 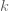 เป็นค่าคงตัว) เป็นค่าคงตัว)
แทนค่า 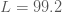 เมื่อ เมื่อ 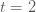 ใน ใน 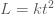
จะได้ 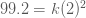 → → 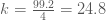
ดังนั้น จะได้สมการเป็น 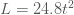
ลูกตุ้มนาฬิกาแกว่งได้นาทีละ 24 รอบ หมายถึง 24 รอบ ในเวลา 60 วินาที
ถ้า 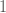 รอบ ในเวลา รอบ ในเวลา 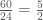 นาที นาที
ถ้า 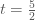 จะได จะได 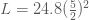
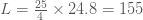
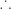 ก้านของลูกตุ้มนาฬิกายาว ก้านของลูกตุ้มนาฬิกายาว 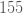 เซนติเมตร ตอบ เซนติเมตร ตอบ

|

